Project leader: Professor Jing An
Project manager: Victor Amaya
Team members: Will Chen, Ethan Ouellette, Nick Sortisio, Shuhuai Yu
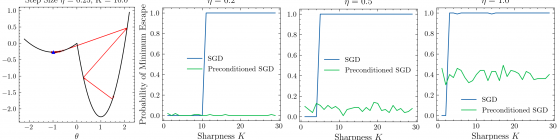
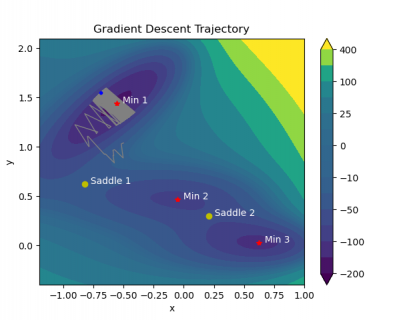
Stochastic gradient descent (SGD) is a popular optimization algorithm used to train large scale machine learning models. Despite its widespread use, there are a lot of unanswered questions about the theory behind its empirical behaviors, especially in so-called “deep” neural networks. Over time people have made improvements on SGD, leading to a variety of SGD variants with different predictive performance and efficiency. In order to understand the performance of SGD variants, we derived mathematical models of these SGD algorithms as stochastic differential equations (SDEs) to study how certain SGD algorithms systematically lead to particular performance characteristics. For example, a wide class of SGD algorithms known as preconditioned SGD are shown to lead to models that do very well on data they have seen before, but perform worse when exposed to a new setting. We also studied the adequacy of different SDE representations of SGD and their implications for the theoretical performance guarantees we can derive, an area of active debate in the field. Our work contributes to our understanding of how SGD and its variants behave theoretically, in order to allow machine learning practitioners to make informed decisions in the process of building models.
Stochastic gradient descent (SGD) is widely used to solve empirical risk minimization problems, especially in training machine learning models, where we are interested in minimizing training loss. Although much is known about the behavior of SGD with a convex loss function, our theoretical understanding of how it behaves in non-convex settings—as is typically the case in deep neural networks—is less developed. Previous research has utilized tools from stochastic analysis by studying stochastic processes that approximate the distribution of SGD. Such approximations are known as stochastic modified equations (SMEs). Our project is interested in using this previously developed mathematical framework to study the stability and minimum selection characteristics of certain stochastic gradient algorithms. In particular, we study a class of SGD variants known as preconditioned algorithms, which may use second order information—usually sparse approximations of the Hessian or empirical Fisher matrix—in order to leverage the geometry of the loss landscape to speed convergence. Specifically, past papers employ a dynamical stability approach to conduct convergence analysis of SGD. We use the same methods to understand other variants of SGD. We provide examples showing why preconditioned algorithms systematically select sharper minima than SGD, leading to a well-documented generalization gap between SGD and its preconditioned variants. There is much active debate on whether or not the noise of SGD in higher dimensions is Gaussian, so we also evaluate the adequacy of SDE representations of preconditioned SGD as Itô and Lévy processes, respectively. Our project identifies and explores the aspects of SGD variant design that lead to their observed performance characteristics, allowing machine learning practitioners to justify their decisions when training machine learning models.