Project leader: Professor David Dunson
Project managers: Tao Tang and Omar Melikechi
Team members: Trevor Bowman, Jenny Huang, Greg Orme, Pranay Pherwani
During an epidemic, it is important to gain an understanding of the intrinsic properties of an outbreak, such as how rapidly it spreads or how many individuals are currently infected. Accurate forecasts about the trajectory of the epidemic rely heavily on an understanding of these basic properties during the early stages of an outbreak. The early-stage outbreak also happens to be when parameters, such as the transmission rate, are the most difficult to pin down. We explore several methods that may allow for better estimation of these parameters. These methods include incorporating known information about the recovery rate of the disease in question and considering a stochastic model which may be more accurate during the early days when case counts are low. Moreover, as seen during the COVID-19 pandemic, transmission rates may change rapidly throughout the course of the epidemic with increased testing or shifts in containment strategies. Hence, we also focus on designing fast and simple methods for detecting a change in transmission rate. Our work is ultimately aimed at helping policy-makers make informed decisions during an early epidemic, such as what types of data (data on asymptomatic spread, recovery rate of the disease, contact network data etc.) would be most effective to collect to gain a good understanding of these basic properties of the disease and thus more accurate forecasts.
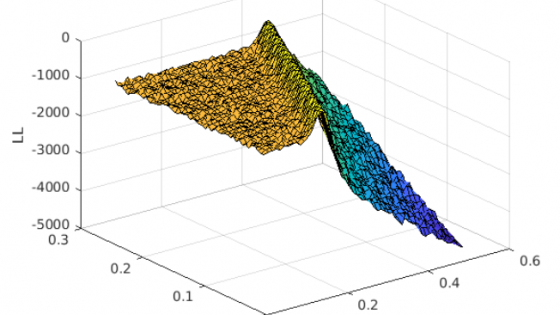
During an early-stage epidemic, there are inherent limitations in the ability to recover parameters in compartmental epidemic models such as the SIR. While the maximum likelihood estimator (MLE) exists when fit on data from the pre-peak epidemic, the curvature of the likelihood in the neighborhood of the MLE is very small in the direction where β (transmission rate) and γ (recovery rate) lie along a line. That is, different parameter values may lead to SIR model trajectories that are nonetheless very "close". We explore several methods to reduce uncertainty in the estimation of these parameters, including placing an informed prior on γ, exploring predictions we are able to make (such as the time until the epidemic curve peaks), and using a stochastic SIR model, which may be more accurate for inference during the early stage when infection events are infrequent. With an informed prior on γ, we also design a fast and simple method for detecting changes in the transmission rate in response to shifts in policy and containment strategies. Our work is aimed at helping policy-makers come to informed decisions early in the epidemic, such as what types of data (data on asymptomatic spread, recovery rate of the disease, contact network data etc.) to prioritize collecting to better understand the basic properties of the outbreak and to gain more accurate forecasts.