This project has been featured on the Duke research blog! Click here for the article by Robin Smith: Modeling the COVID-19 Roller Coaster.
Project leader: Professor Rick Durrett
Project manager: Hwai-Ray Tung
Team members: Laura Boyle, Sofia Hletko, Jenny Huang, June Lee, Gaurav Pallod
This project has produced the following paper:
Laura Boyle, Sofia Hletko, Jenny Huang, June Lee, Gaurav Pallod, Hwai-Ray Tung, and Richard Durrett, Selective sweeps in SARS-CoV-2 variant competition, Proceedings of the National Academy of Sciences volume 119, number 47 (2022).
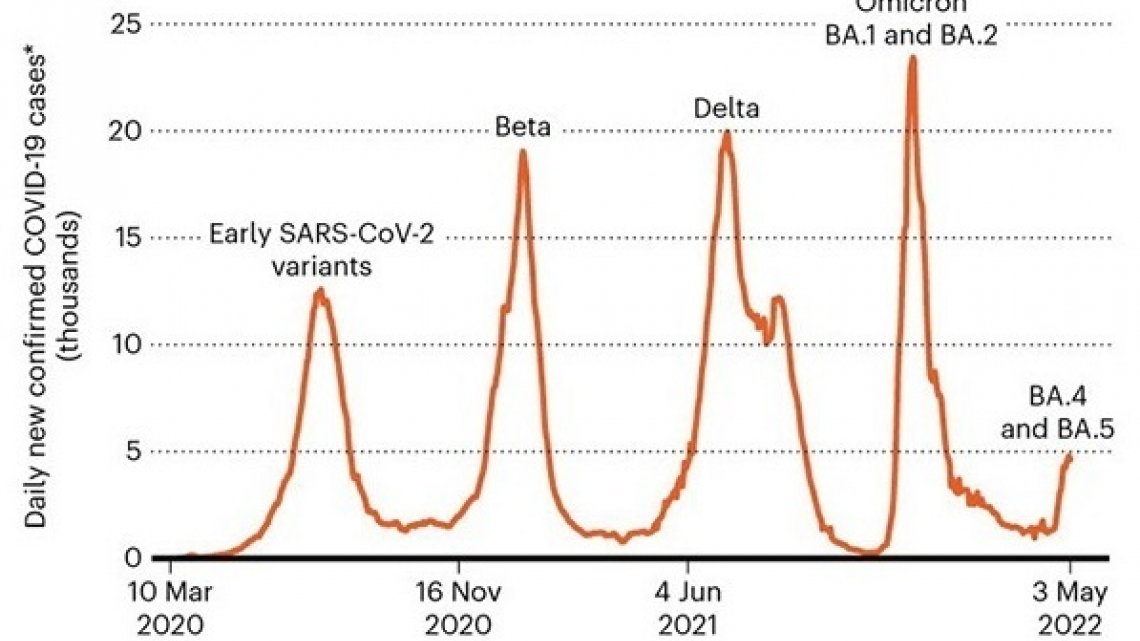
The graph below shows the course of the covid epidemic over the last two years. The virulent Delta strain stressed hospitals to the breaking point but was later replaced by the more transmissible but less deadly omicron family. The BA.1 and BA.2 strains emerged in South Africa in Oct 2021. Two of their children B.1.1.529 and BA.2.12.1 (named based on their positions in the phylogenetic tree of variants) turned out to be especially transmissible leading to a large spike in cases. Finally just as the DOMath program was beginning in May 2022, twin strains BA.4 and BA.5 that could infect individuals that has been infected with earlier omicron strains began to emerge.
The aim of this project was to use mathematics to understand the observed patterns of covid variant evolution. The simple answer is that change of variables in the ODE for the competition of covid variants shows that the fraction of cases due to the new strain $x(t) = I_2/(I_1+I_2)$ satisfies the logistic differential equation
$$x'(t) = \lambda(t) x(t)(1-x(t))$$
which models the takeover of a population by an advantageoues mutation. Here
$$\lambda = (\beta_2-\beta_1) s(t) +\theta \beta_2 r_1(t)$$
where the $\beta_i$ are infection rates for the two strains, $s(t)$ is the fraction of the population that is susceptible, $r_1(t)$ is the fraction immune to the first strain, and $\theta \beta_2$ is the rate at which the second strain can infect individuals immune to the first either due to prior infection or vaccination.
From fitting our model to SARS-CoV-2 variant data, we found that the rapid turnover from one dominant variant to another fits a logistic curve quite well (see plot above). Our model also allows us to estimate the fitness advantage, $\lambda$, of one strain over another. The two components of the fitness advantage in the formula for $\lambda$ are: (i) an increase in transmissibility due to advantageous mutations in the spike protein (ii) the ability to cause crossover infections due to reduced sensitivity to host immune responses from previous infections. While the formula for $\lambda$ emerged from calculus, our conclusions agree with infectious disease experts: "As gains in infectivity start to slow, covid variants maintain their fitness by overcoming immunity''.