Project leader: Professor Colleen Robles
Project manager: Chun-Hsien Hsu
Team members: Yannan Bai, Annapurna Bhattacharya, Stavan Jain, Kurt Ma, Ricardo Prado Cunha, Anoushka Sinha
A mathematical proof is a logical argument that aims to establish the validity/soundness of a mathematical claim. Traditionally, mathematical proofs have been done using intuitive reasoning and natural (i.e. spoken) language. Such informal proofs rely on the reader’s interpretation and cannot be verified algorithmically. Formal proofs, on the other hand, are written using precise rules and syntax which allows every assumption and claim made within a proof to be checked by a computer, and demands that all such assumptions and claims be justified using predefined rules. Proofs written formally are thus much more rigorous and certain. The verification of a formal proof is done using a proof assistant: software that helps in developing and checking mathematical proofs. For our project we worked with one such proof assistant: Lean. Lean is open source software which allows encoding formal proofs in its own functional programming language. Using Lean we have been working on developing a teaching aid for Duke’s introductory linear algebra course—Math 221. It plays out like a game and allows students to write formal proofs in linear algebra.
We hope that our “linear algebra game” will serve the dual purpose of introducing students to formalization and give them a more thorough understanding of the assumptions that go into writing the proofs that they do in class.
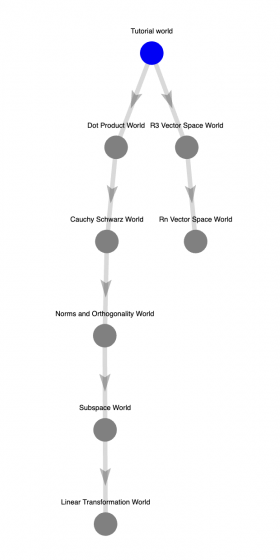
The practice of writing clean, rigorous proofs is a challenging point for prospective mathematics majors as they transition from the highly procedural mathematics in high school to the more abstract, proof-oriented body of knowledge introduced in college mathematics. In our project, we developed a supplementary resource called “The Linear Algebra Game” intended for a typical introductory linear-algebra course, such as Math 221 at Duke, to help students make the transition towards proof-based mathematics. As opposed to the human-language based proofs we normally see in textbooks, homeworks, or exams, our linear algebra game uses a functional programming language called Lean as the means to write proofs. The students using our tool would learn linear algebra while producing completely formalized proofs, proofs that are precise, rigorous and lack any ambiguity. Through the 8 worlds, and 64 different levels (each with 1 proof), we hope the students will better understand the logical structure and the requirements to write complete proofs in mathematics. In addition to “The Linear Algebra Game”, we also contributed some missing definitions and lemmas to Lean Mathlib. Mathlib is a library of formalized mathematics in Lean which is meant to serve as a starting point for mathematicians who wish to use Lean for research. The definitions we contributed are the orthogonal complement and orthogonality for affine subspaces (which are quite similar to their vector space counterparts), as well as a multitude of related lemmas, as requested by the Mathlib maintainers. Some of the more interesting lemmas are that a subspace is empty or a singleton iff its complement is the universe, that orthogonal complements through different points are parallel, and that orthogonal complements of parallel subspaces through the same point are equal.