Project leader: Professor Haohua Deng
Project manager: Chongyao Chen
Team members: Ronan Hallinan, Erick Jiang, Santino Panzica, Felicia Wang
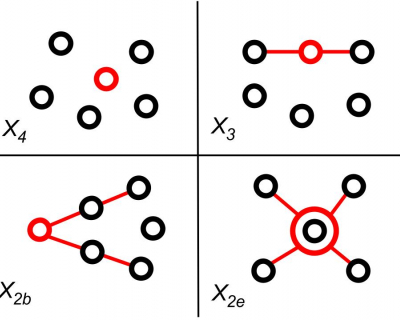
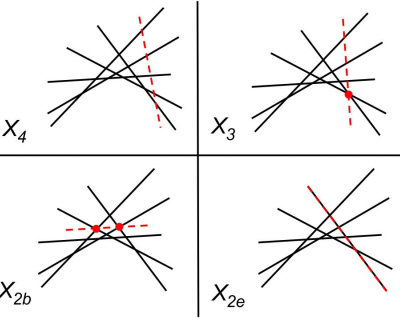
Our project aimed to investigate the properties of a particular algebraic concept called moduli spaces. Intuitively, moduli spaces "parametrize" certain types of mathematical objects—in our case they parametrize "weighted stable hyperplane arrangements." Moduli spaces have many connections to deep topics within algebraic geometry, but we attempted to examine them using largely undergraduate-accessible techniques. We were particularly interested in the boundaries of these spaces, which is where their "nice" properties start to degenerate, and how various functions behaved on these boundaries.
In our project we took a combinatorial approach towards characterizing the moduli spaces of weighted stable hyperplane arrangements in complex projective space. Instead of viewing stability as an algebraic condition on Weil divisors, we considered numerical restraints—being log canonical and the log-Calabi Yau condition—that were more suitable for combinatorial analysis. Our principal focus was characterizing the fibers of points within the image of the forgetful mapping, exploring how their boundaries degenerate under collisions induced by fixing various weight vectors.