Project leader: Professor Ruda Zhang
Project manager: Yixin Tan
Team members: Noah Harris, Matt Robbins, Marie-Hélène Tomé
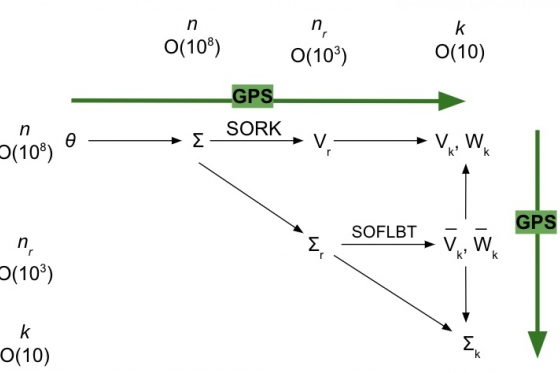
Our project revolved around approximating subspace-valued functions, i.e., rules assigning some parameter to a set of vectors forming a basis for a subspace. The applications of this include reduced order modeling where subspaces are used to model complex systems in a more computationally efficient manner by reducing the dimension of the matrices used to mathematically represent the system. Instead of recomputing the subspaces needed through different kinds of model reduction methods, approximating the subspace-valued map directly from the parameter to the subspace cuts out all of this computation. Given some data about the mapping, we approximate the function from the parameter to the subspace so that we can get a good prediction of the function value, i.e., the bases needed for model reduction, at a new value of the parameter for which we have not computed the function value. This is especially useful in modeling second order systems where multiple model order reduction methods are used to create the final reduced order model. Our work helps to give theoretical guidance as to when GPS will work well, i.e., when you come up with a new combination of model order reduction methods, is GPS suitable to approximate this new variant?
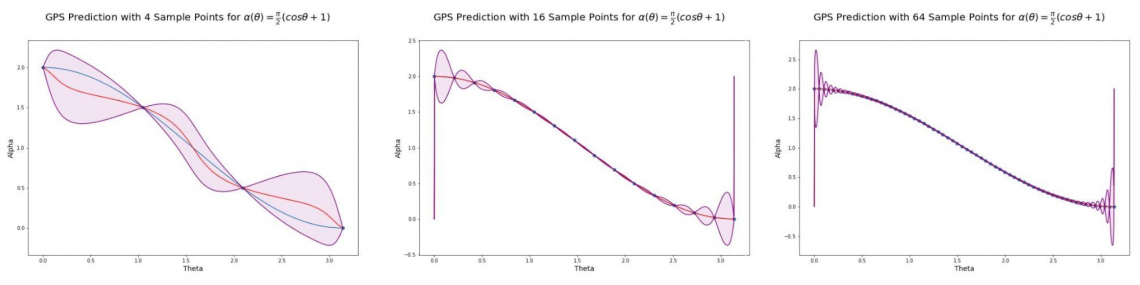
We applied Gaussian Process Subspace (GPS) prediction for general subspace valued maps to reduced order modeling. To begin we studied various classical methods of reduced order modeling and proved that when the initial Linear Time Invariant (LTI) system is a $C^k$ function of a parameter space, $\Theta \subset \mathfrak{R}^d$, the reduced system generated by a particular method of model order reduction has a particular smoothness structure. We found that for different methods of model order reduction we could create stronger results regarding the smoothness of the reduced system. Once we proved smoothness, we made predictions using GPS. We numerically created sample points, each point consisting of parameter values and a basis for a subspace, for both model order reduction methods and smaller problems. For each case, most sample points were used to create GPS models for the respective problems and the rest were used to test the error of our models. We computed the original model for the new value of the real parameter theta and then used GPS to approximate the function mapping to the bases, get the probabilistically predicted bases, and associated uncertainty quantification, and then used the two predicted bases together with the original model to get the approximate reduced order model. We then quantified our error using the Grassmann Distance, a common metric for the Grassmann Manifold, and found sample sizes such that our model was reasonably accurate. The distance between subspaces is essentially rotations, i.e., how much do we have to rotate for the subspaces to be aligned? For the Grassmann manifold of dimension $k$, the distance between two subspaces is maximally $dist(X, Y) \leq \pi/2 \sqrt{k}$. We add a spectral separation assumption for the entire domain we are approximating. A separated spectrum guarantees a good result with GPS. Once a spectral crossing occurs, the subspace-valued function may not even be continuous and, therefore, the approximation will be poor. This affects GPS prediction accuracy since a discontinuity, or finite jump, can cause large prediction errors. If a function is smooth, continuous or not continuous this makes a difference for the prediction accuracy of GPS. Our numerical results show that GPS works well for analytic functions, has higher sensitivity to perturbations in the smooth case, and has the highest sensitivity in the discontinuous case. Our work gives theoretical guidance as to when GPS will give good approximations. This is applicable to reduced order modeling since a composition of multiple model order reduction methods is often necessary to arrive at the final reduced order model. Our work helps to answer the question: when will GPS give good approximations to subspace-valued maps resulting from the composition of a new combination of model order reduction methods.