Update, June 2021: the Quanta article "Mathematicians find long-sought building blocks for special polynomials" includes a DOmath connection: the breakthrough work in number theory by Duke professor Samit Dasgupta uses a computer program written by two of his students, Max Fleischer and Yijia Liu, building on their 2020 DOmath project.
The 2020 DOmath program ran virtually from May 18 to July 10, 2020. Here are the six projects, along with the teams' summaries of what they accomplished.
Modeling Covid-19, led by Professor Rick Durrett
Of the basic epidemic models on graphs that can dynamically represent social networks in homogeneously mixed populations, the most relevant is the SEIR model. Individuals are first classified as Susceptible to disease, later reclassified as Exposed (if they have the disease but show no symptoms), Infected (if they have the disease and are contagious), and finally Removed (if either recovered from the disease or in quarantine or in the hospital). In our project we further extended the question of Covid-19’s impact to college campus policies, investigating a number of questions but here highlighting only two.
Materials science problems: numerical methods and techniques, led by Professor Saulo Orizaga
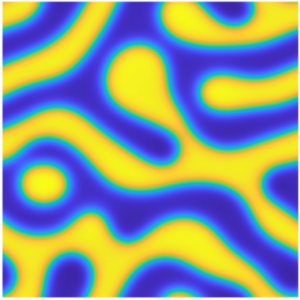
The Cahn-Hilliard equation is a partial differential equation (PDE) that models phase separation, which observes the behavior of materials at the liquid or solid state in a mixture. One of the simplest examples of this phenomenon is the mixing of oil and water; in this case, oil and water will separate and segregate into distinct regions over time, and continue until the two substances are completely separated. The Cahn-Hilliard equation also has many important applications in physics, engineering, and medicine. Since the Cahn-Hilliard equation includes nonlinear terms, the PDE cannot be solved directly and numerical methods are required to estimate a solution. As such, we must develop accurate and efficient methods to model such behaviors. This summer, we further developed, analyzed, and compared four methods and their variations to find a preferred numerical method, considering its efficiency, stability, and the energy decreasing property.
Enriched Euler numbers for line bundles, led by Professor Kirsten Wickelgren
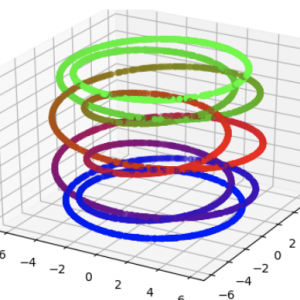
Euler classes are used to help distinguish between line bundles over topological spaces and their algebraic analogs. Over the real numbers, the classical Euler class is computed by the Brouwer degree of a section “s”. If “s” intersects the zero section with positive slope, this intersection point contributes +1 to the Euler class; if “s” intersects the zero section with negative slope, this intersection point contributes -1 to the Euler class. Using this formula, one can show that the cylinder has Euler class 0, while the Möbius strip does not have Euler class 0. In particular, the cylinder and the Möbius strip are not the same line bundle.
Neural network dimension reduction of data with topological constraint, led by Professor Xiuyuan Cheng
Working with “big data” is a hot trend in many fields of research and industry. From selfies to stock markets, many aspects of life have an abundance of data, with each data point having a massive amount of different features, or dimensions, to it...
Decomposition of class groups and representation theory,
led by Professors Samit Dasgupta and Jiuya Wang
In this DOMath project, we studied the structure of class groups by representation theory, with a particular emphasis on various decompositions of representations of finite groups.
Groups are fundamental mathematical structures that describe the symmetry of mathematical objects. Representation theory studies how groups act as linear transformations. Class groups are the central objects in modern number theory. The mystery of class groups has inspired many different branches of number theory. Since class groups of number fields are naturally equipped with linear actions from the Galois group, the symmetry group of a number field, we can study class groups using representation theory...
PDE modeling of collective motion, led by Professors Alexander Kiselev and Siming He
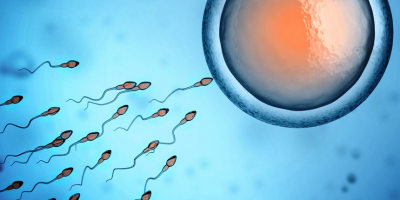
Inspired by recent experimental studies of cell motility and locomotory behavior in fluid environments, our project models the interaction between a sperm and an egg in a fluid medium. More specifically, we are concerned with how shear flow and chemotaxis affect the expected time it takes for a sperm dispersing randomly according to Brownian motion to reach an egg...