The Rudin Prize
2024 Prize Recipients
Shreya Arya: Geometry of Stratified Spaces for the Analysis of Complex Data
Traditionally, statistical data has been in the form of elements of Euclidean space. With increasing technological advances, data is becoming increasingly complex, not only in terms of size but also structure, so it is assumed to lie in lower-dimensional non-linear spaces such as smooth manifolds. Nonetheless, real-world data is not always in the form of smooth manifolds. For example, the space of trees, shapes, and positive semi-definite matrices, and more generally orbit spaces of manifolds, can have singularities. Despite numerous examples, the mathematical foundations for probability and statistical analysis are lacking on such spaces. In this thesis, we explore the geometry of data valued in stratified spaces with the overall objective of enabling statistics on these spaces.
Specifically, we first provide an algebraic model of shape space (or the space of stratified spaces) with the objective of shape analysis and comparison. The foundation of this construction relies on the topological analogue of the Radon transform, building on the work of Schapira who showed that such transforms are injective. Secondly, we provide a starting point to define diffusion on stratified spaces. On Euclidean spaces, Brownian motion is
constructed by taking scaled limits of random walks. This approach is challenging because not only are stratified spaces non-linear but also their tangent spaces are non-linear, unlike smooth manifolds. So, instead, we define Brownian motion on stratified spaces by taking appropriate limits of Dirichlet forms and show that they converge appropriately for certain subanalytic sets.
Chun-Hsien Hsu: Poisson Summation Conjecture on Braverman-Kazhdan spaces
My research lies in the intersection of harmonic analysis and number theory. In number theory, one major problem is to prove the meromorphic continuation of L-functions. For the Riemann zeta function, its meromorphic continuation was proved using the Poisson summation formulae on a one-dimensional vector space. Braverman and Kazhdan have observed that if one could establish Poisson summation formulae on certain family of singular spaces, then one could prove analytic properties of L-functions in great generality. My thesis establishes the local Fourier theory on some singular spaces such as cones and confirms many expectations of the Poisson summation conjecture.
In my joint work with J. Getz. and S. Leslie, we give an analytic definition of Schwartz spaces on each Braverman-Kazhdan space, the affine closure of the quotient of a simply connected simple group by the derived subgroup of a maximal parabolic. Furthermore, we discover nice formulae for the Fourier transforms. As it turns out, these formulae look alike those on the vector spaces, except that it needs to be properly normalized due to the existence of singularity on Braverman-Kazhdan spaces. In the nonarchimedean setting, I further give representation theoretic descriptions of Schwartz spaces and confirm various structural properties of Schwartz spaces.
2023 Prize Recipients
Sven Hirsch: Intermediate curvature, spacetime harmonic functions, and the monotonicity of the Hawking energy
It is well-known that the sum of all angles of a triangle in a plane equals 180 degrees. This is a special case of Gauss-Bonnet's theorem from 1848 which states that in Dimension 2 the integral of a surface's curvature equals its Euler characteristic. Results of this type are central to understand the interactions between geometry and topology and have also found far-reaching applications in Einstein's General Relativity. In higher dimensions, the resolution of Geroch's conjecture, resolved by Schoen-Yau in 1979 for $n\le7$ and Gromov-Lawson in 1983 in general states that the torus $T^n$ does not admit a metric of positive scalar curvature. Similarly, it follows from Bonnet-Myer's theorem from 1941 that $M^{n-1}\times S^1$ does not admit a metric of positive Ricci curvature. However, most other topological spaces are still not well understood in terms of their curvature. For instance, Hopf's conjecture, the question whether $S^2\times S^2$ admits a metric of positive sectional curvature, remains open for nearly a century. In a joint work with Simon Brendle and Florian Johne we add more topological spaces to the above list, and show that for $n\le7$, manifolds with a non-zero degree map onto $M^{n-m}\times T^m$ do not admit a metric of positive $m$-intermediate curvature.
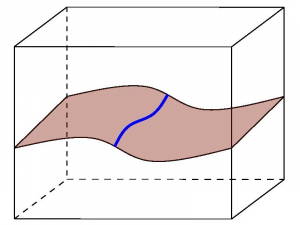
Our proof is based on tools from geometric measure theory, PDE and topology. More precisely, we prove the existence of stable weighted slicings as depicted in the figure to the left. A weighted slicing consists of a collection of homologically non-trivial surfaces $\Sigma_m^{n-m}\subset\dots\subset \Sigma_1^{n-1}\subset\Sigma_0^n=M^{n-m}\times T^m$ minimizing weighted area functionals together with a collection of weight functions $u_i$, $i=1,\dots,m$, solving certain PDEs. In the figure the cube represents the manifold $\Sigma_0=M^{n-m}\times T^m$, and $\Sigma_1$, $\Sigma_2$ are the surfaces in red and blue respectively. Combining the stability of the slicing with delicate gradient and extrinsic curvature estimates then yields our result.
Langxuan Su: Absolute Continuity of Singular SPDEs and Bayesian Inference on Dynamical Systems
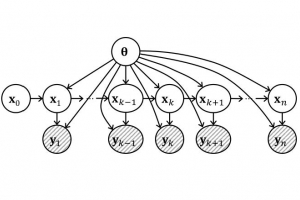
My dissertation explores the interplay among probability, stochastic analysis, and dynamical systems. In the first part, I study infinite-dimensional dynamical systems with random noise, in particular, stochastic partial differential equations (SPDEs). These systems arise from fluid mechanics, acoustics, gas dynamics, and so on. It is a classical problem to analyze how random noise spreads through the system, whether the noise is ``twisted’’ by the nonlinear dynamics or stays ``qualitatively the same” as without the nonlinear dynamics. Jonathan Mattingly, Marco Romito, and I show that in stochastic Burgers equations, the noise stays ``qualitatively the same”, illustrating the fundamental probabilistic structure of this class of SPDEs. In the second part, I work on Bayesian inference on dynamical systems. As introduced in a statistics course, Bayesian inference refers to the following procedure: starting with some prior beliefs on parameters (the theta in the picture), one updates the posterior belief on parameters based on observed data samples (the y in the picture). This procedure has not been justified if data are generated from general dynamical systems (the x in the picture). Sayan Mukherjee and I develop a unified framework to do Bayesian inference with theoretical guarantees on a wide range of dynamical systems.
More precisely, in the first part, we prove that the law of the singular stochastic Burgers equation is absolutely continuous with respect to the corresponding stochastic heat equation with the nonlinearity removed. To handle spatially rough (singular) solutions, we introduce a novel decomposition in the spirit of Da Prato-Debussche and Gaussian chaos decomposition, by separating out the noise into different levels of regularity. At each level, we apply an extension of Girsanov’s Theorem to remove the nonlinear term. This result illustrates a notion of ``ellipticity'' in the infinite-dimensional setting. In the second part, we establish connections between large deviations and generalized Bayesian inference on dynamical systems. As an application, we prove new quenched/annealed large deviation asymptotics and Bayesian posterior consistency for a class of mixing stochastic processes and classical deterministic dynamical systems. In the case of Markov processes, one can seamlessly check conditions for posterior consistency, given estimates for the log-Sobolev constants, which makes our framework a black box.
2022 Prize Recipient
Stephen McKean: Local Contributions in A^1-Enumerative Geometry
There is a close connection between algebra and geometry. In middle school or high school, we learn how to graph equations, and we practice recovering an equation from its graph. A shape is called an algebraic variety if it is the graph of a polynomial equation. A lot of information about an algebraic variety can be predicted just by looking at its associated polynomial. For example, if I give you two polynomials, I might ask how many times their graphs will intersect each other. This is answered by Bézout’s theorem: take the largest exponent on each of the polynomial equations and multiply them together to get the total number of intersections. However, there is a problem with Bézout’s theorem — it only works over number systems that behave like the complex numbers. If I try to use the real numbers, rational numbers, or a finite number system, there will be counterexamples to Bézout’s theorem. My thesis fixes this problem by giving a weighted count of intersections.
Instead of giving an integer-weighted count, intersections are weighted by bilinear forms. These bilinear forms arise naturally in motivic homotopy theory as a generalization of the Brouwer degree from algebraic topology. In my thesis, I show how to assign such a bilinear form to an intersection point in terms of the geometry of the algebraic varieties at the given intersection. One can then recover classical results from this bilinear form: its rank gives the intersection multiplicity over algebraically closed fields, and its signature gives an oriented or mod 2 intersection multiplicity as seen in differential topology. We can also deduce some new, arithmetic data about these intersections by taking Hasse—Witt invariants over number fields, discriminants over finite fields, and so on.
2021 Prize Recipient
Lihan Wang: Quantitative Analysis in Stochastic Homogenization and Hypocoercive PDEs in Sampling
I am an applied mathematician working in the interface between partial differential equations, probability and numerical algorithms. The first aspect of my research is called stochastic homogenization. The conductance of a material can be highly heterogeneous at a molecular level (see picture), and therefore any direct simulation is computationally undesirable since the variations on small scales need to be addressed. However, if we further assume the material to have some spatial homogeneity in statistical information, then we may make approximations by simulating some homogeneous material, so that computational cost can be significantly reduced. In the first part of my thesis, which is joint work with professors Jianfeng Lu and Felix Otto, we study the approximation of three-dimensional infinite material, and give an optimal algorithm that successfully captures the correct scaling of error induced by truncation and randomness.
The second part of my thesis, which consists of joint works with Yu Cao (former Duke math PhD student) and Jianfeng Lu, is about sampling from a target distribution, which has profound relationship with optimization, statistics, molecular dynamics and machine learning. A popular approach to sampling consists of using continuous time Markov Chain Monte Carlo processes: after running a stochastic process for a long time, its distribution will be close to the target. Therefore, studying the convergence rates of these processes is important for applied mathematicians, since processes that converge fast have a practical advantage. In the second part of the thesis, we give sharp estimates on the convergence rates of several sampling processes, including the underdamped Langevin dynamics, randomized Hamiltonian Monte Carlo, the zigzag process and the bouncy particle sampler. Our results in underdamped Langevin dynamics improve on previous results of many great mathematicians including Cédric Villani.
2020 Prize Recipient
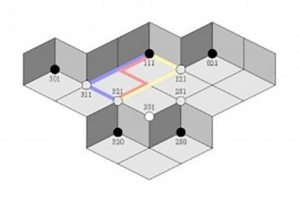
Erika Ordog: Minimal Resolutions of Monomial Ideals
My research lies at the intersection of commutative algebra, combinatorics, and topology. I study higher-order algebraic ramifications that arise from systems of polynomial equations in which each equation sets a monomial — that is, a polynomial with one term — equal to 0. These systems and their higher-order consequences have intricate but concrete combinatorial structure. When the monomials are in three variables, for example, they can be visualized using staircase diagrams like the one pictured below. In these pictures, as in the more general case of arbitrary numbers of variables, staircase diagrams encode information about how the monomials relate to each other. As part of work for my dissertation, John Eagon, Ezra Miller, and I gave a full solution to a central problem that has been open in the field since the early 1960s. The solution involves summing over lattice paths (like the ones in the picture) along the grid lines between appropriate points on the staircase.
To be more precise, given any monomial ideal in finitely many variables, we construct a free resolution that is canonical, minimal, universal, closed form, and combinatorial. We call this the canonical sylvan resolution. The differentials are weighted sums over lattice paths whose weights come from higher-dimensional analogues of spanning trees in simplicial complexes indexed by integer vectors. This construction works over fields of characteristic zero and most positive characteristics. Over a field of any characteristic, we also construct more efficient noncanonical sylvan resolutions, whose differentials sum over noncanonical choices of these generalized spanning trees at points along the lattice paths.