Project leaders: Professors Samit Dasgupta and Jiuya Wang
Project manager: Pam Gu
Team members: Zizai Cui, Max Fleischer, Yijia Liu
In this DOMath project, we studied the structure of class groups by representation theory, with a particular emphasis on various decompositions of representations of finite groups.
Groups are fundamental mathematical structures that describe the symmetry of mathematical objects. Representation theory studies how groups act as linear transformations. Class groups are the central objects in modern number theory. The mystery of class groups has inspired many different branches of number theory. Since class groups of number fields are naturally equipped with linear actions from the Galois group, the symmetry group of a number field, we can study class groups using representation theory.
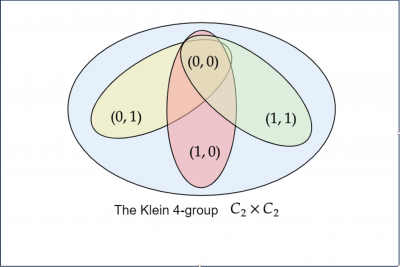
Decomposition is a universal idea and tool in mathematics that reduces a more complicated object into simpler ones. For example, you can decompose integers into prime numbers and polynomials into irreducible polynomials. Similarly, we can decompose a representation into smaller pieces. Classically, a result by Artin states that every representation can be decomposed into a linear combination of 1-dimensional induced trivial representations. We ask the following question: for what types of groups do we get such a linear combination with positive coefficients.
Our question is motivated by a recent progress in bounding ℓ-torsion of class groups for number fields. This type of decomposition of class groups with positive coefficients turns out to be a crucial input that makes this new result possible. Therefore, our goal is to give a complete classification of all finite groups that admit this type of decomposition.
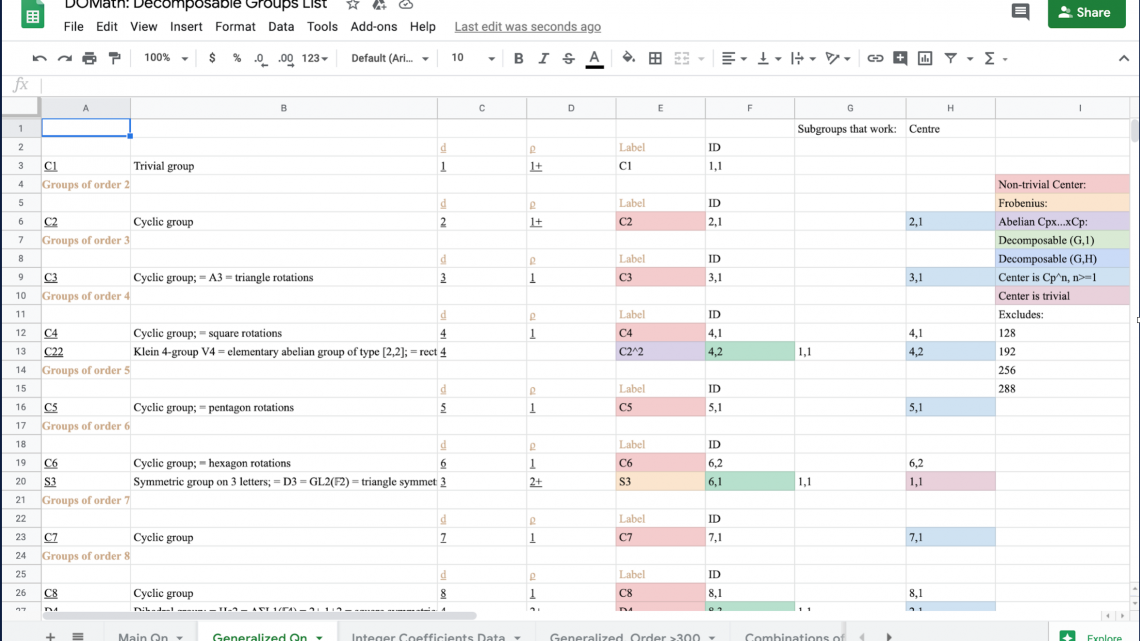
We approach the question in both numerical and theoretical ways. A modern computer algebra system, Sage, was helpful, since it has a database on all finite groups with small degrees. We used Sage to find patterns in small groups during our research. Theoretically, we succeed in giving a full classification of all finite groups that admit a decomposition with positive coefficients, by relating this representation theory question to a group theoretic question: partitionable groups, which was studied and solved in the1960s. We also studied a natural generalization of this problem that is equivalent to a more general class group question, and another extension of this problem which requires the coefficients to be both positive and integral. We have been making steady progress in all mentioned directions and hope to get the answer in full generality.