Project leader: Professor Xiuyuan Cheng
Project manager: Ziyu Chen
Team member: Bhrij Patel
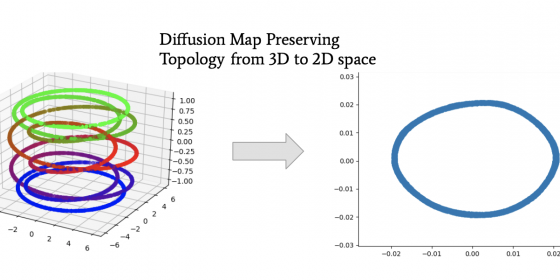
Working with “big data” is a hot trend in many fields of research and industry. From selfies to stock markets, many aspects of life have an abundance of data, with each data point having a massive amount of different features, or dimensions, to it. A 28 x 28 pixel image can be interpreted as a 784 dimensional list of numbers, with each number representing a pixel value. The idea of dimension reduction is to take data and compress it down to lower dimensions, so for example, instead of representing each image with 784 numbers, reduce it down to 2 numbers. This process is useful for sending images across the internet as it needs to carry less information. Different dimension reduction techniques perform differently based on how the data is “shaped”. Even though we cannot visualize past three dimensions, data still has structure, referred to as its topology. Some reduction techniques do not preserve that topology when compressing down to lower dimensions, causing poor reconstruction of the original data. The image compressed to 2 numbers could differ greatly when reconstructed back up to 784 dimensions (not good!). There are some reduction techniques like diffusion mapping (see picture below) that can preserve topology well.
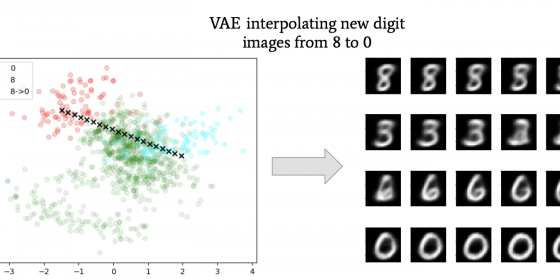
However, they only lower dimensions, they cannot bring data back up to higher dimensions. So, having an image stay as only two numbers is not quite as interesting to look at. However, there are neural network algorithms called Variational Autoencoders (VAEs) that can lower and raise dimensions of the original data. They even can create new data from the lower dimension space, a process known as out-of-sample extensions (see picture below). However, VAEs do not preserve topology as well as diffusion maps as when it comes to data that are “shaped” like spirals. Therefore, the reconstructed data will not look like the original. The goal of this project is to create models from VAEs that will bring high dimensional data to lower dimensions while still preserving the topology to more accurately reconstruct data of all types of “shapes”. This summer we performed reconstructions and interpolations with VAEs on different datasets, and we also compared embeddings by VAEs to diffusion maps. When compressing the MNIST Handwritten Digit Image dataset down to 2 dimensions, the data areas of different numbers overlapped, as in points representing 3 overlapped with those representing 2 for example. Thus, construction of those points resulted in an image that looked like a blend of 3 and 2 (2nd picture). This overlap of labels did not occur when we compressed down to 20 dimensions. For spirals with low frequency and paraboloids, VAEs had lower reconstruction errors than with spirals of higher frequencies. Going from 3 to 2 dimensions, we also observed that diffusion map embeddings preserved the topology of S^1 manifolds (think “circles”; 1st picture), thus meaning that diffusion maps can reveal the topology in their embeddings. These results could not be reproduced by VAEs.