Project leader: Professor James Nolen
Project manager: Oliver Kelsey Tough
Team members: Brian Glucksman, Shan Zhong
Project summary:
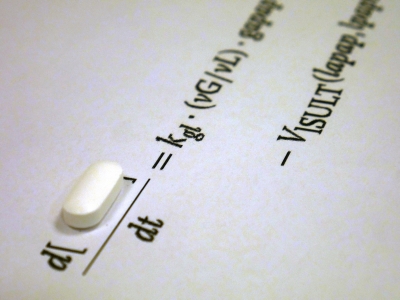
We use an ordinary differential equation model with random parameters to understand the biochemical mechanisms of liver failure caused by acetaminophen overdose. Acetaminophen, found in a number of over-the-counter drugs including Tylenol, is the most widely used painkiller in the world. It is metabolized in the liver where the toxic byproduct NAPQI is produced. Though it is safe to take acetaminophen at therapeutic doses, acetaminophen overdose is the leading cause of acute liver failure in the US. Researchers have modeled the effects of acetaminophen on the body with ordinary differential equations. Several of these differential equations include a Michaelis-Menten term to model a biochemical reaction, which is constrained by a maximum velocity. Existing models take maximum velocities as constants, but in reality these velocities vary on average 25% from individual to individual. We built a model that varies all maximum reaction velocities according to a uniform random variable, which we used to simulate acetaminophen exposure of several different virtual individuals. This new model, which involves 25 differential equations, allowed us to perform singular-value decomposition and principal component analysis to identify the most influential reaction velocities. Optimizing the treatment is a non-convex optimization problem in high dimensions. We used a random walk algorithm to search for the optimal treatment for 22g of acetaminophen. Moreover, we verified that the treatment protocol widely used today is suboptimal.
Download the report: "ODEs with random parameters"