Project leader: Professor Alexander Watson
Project manager: Kevin Stubbs
Student researchers: Muthu Arivoli, Norah Tan, Chongbin Zheng
Project summary:
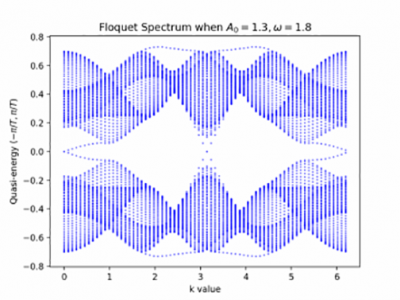
We started by looking at the Su-Schrieffer-Heeger (SSH) model, which describes a one-dimensional chain of atoms with staggered hopping amplitudes. We saw that the existence of edge states in the model is related to a topological invariant of the bulk called the winding number. We then looked at the Haldane model, a two-dimensional tight-binding model in a hexagonal lattice. Again, we found that a topological invariant called the Chern number predicted the existence of edge states. With a nonzero Chern number, two curves emerge from the upper and lower bands, which are otherwise gapped, and cross over at zero, making the material conduct electricity on the edge. After this we investigated Floquet topological insulators, a group of materials that behave like topological insulators from the application of periodic driving. We examined two models, the Rudner model and the graphene-light model. For each, we studied their Floquet spectra, the equivalent of eigenvalue spectra for periodically driven systems, and constructed corresponding topological invariants to study the edge states. Finally, we studied the full PDE model of the graphene-light case without making the tight-binding approximation, confirming the validity of the approximations we employed.
Download the project report: "Floquet topological insulators"