From sports analytics to game theory, and cryptography to diseases, the Department of Mathematics offers a unique set of classes to challenge and engage our students. Below is a sampling of Featured Courses we are currently offering. Please refer to our complete Course listing to see all our classes, plus refer to DukeHub for exact course times and instructors.

What is democracy? More specifically, how does one create rules for elections which have outcomes most consistent with democratic values? The magnitude of the game theory of the single vote ballot in democracies that use it is huge: the two party system, the need for political primaries, obstacles facing 3rd party candidates, and how voters are “throwing their votes away” when they vote for them. This is not inherent to democracy. This is the game theory of the single vote ballot. Alternatively, using preferential ballots in elections is a natural idea since it allows voters to express a 1st choice, a 2nd choice, a 3rd choice, etc. on each ballot, thereby collecting more information from each voter and creating the potential for an outcome which better represents the voters. However, there are many ways to determine the winner of a preferential ballot election, and each “preferential ballot vote counting method” has its own game theory, both for the candidates and the voters, some better and some worse, and often very different from the game theory of the single vote ballot. So which preferential ballot vote counting method is the best? Does there exist a vote counting method which incentivizes politicians to seek out centrist, consensus building positions and to focus on issues important to voters, more than game theoretic tactics meant to manipulate the electorate? Or is there another goal we should be pursuing? In this course, we’ll use game theory and mathematics to study these questions.

Introduction to topics in mathematical cryptography, and the role of cryptography within society, in both historic and modern contexts. Cryptographic systems studied will include: early historical ciphers; the Enigma machines of WWII; modern public channel cryptography. Students will learn: to encode/decode using each system; to quantify the complexity, strength, and weaknesses of each system; to use elementary techniques from combinatorics, graph theory, abstract algebra, and number theory; about the role cryptography plays in human society. Open only to students in the FOCUS program.

This course explores contemporary concerns in the sports world through a data science lens. We apply probability, statistics, machine learning, and simulation tools to investigate issues of fraud detection, "hot hands," team composition, game strategy, and player compensation among other concerns.
Optional lab section for Math 218: solving systems of linear equations, matrix factorizations and fundamental vector subspaces, orthogonality, least squares problems, eigenvalues and eigenvectors, the singular value decomposition and principal component analysis, applications to data-driven problems. Intended primarily for students in computer science and other data-focused sciences.

This is an introductory programming course in Python providing a foundational background for scientific computing. The fundamentals of programming are covered, including memory storage, recursion, basic data structures, and object oriented programming, along with learning how to write effective code in Python. A variety of numerical methods are introduced with a focus on practical implementation, through a broad survey of applications such as physical modeling, data analysis, and optimization.
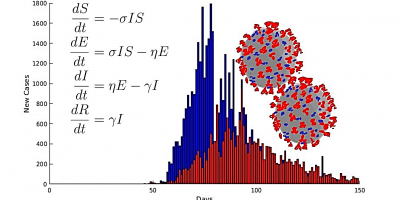
The study of disease has over the past decades benefited tremendously from the field of mathematics. This is in part due to the increase in the availability of clinical and epidemiological data and in part due to more effective training of researchers at the interface between medicine, mathematics, and statistics. The aim of this course is to show undergraduate students how mathematics can be used to further our understanding of human disease. In Fall 2021, this special-topics course will focus primarily on mathematical modeling of the COVID-19 Coronavirus pandemic that has rapidly spread around the world and is now effecting the lives of all people. We will discuss and analyze current mathematical models that are being used to understand and predict the spread of the disease and to inform policy makers about the possible efficacy of mitigation strategies. Some of the time will be spent developing the mathematical ideas needed for application to epidemiological models. The mathematical content will include selected topics from ordinary differential equations (including nonlinear systems of ODEs) and probability, as well as data science. Students will learn how mathematics is being used to make predictions about the current COVID-19 pandemic. While most of the course will focus on the current COVID-19 pandemic, we will also cover mathematical analysis of models for other human diseases, if time permits.
The mathematical theory of algorithms and graphs and their practical implementations. Examines the foundational mathematical structures for the behavior and analysis of algorithms from a variety of domains, with a particular emphasis on graphs. Students tie theory to practice by writing code to implement algorithms, and compare experimentally observed run-times to those predicted by the mathematical theory

Introducing both domain knowledge and quantitative methods for analyzing omics, multi-omics data, and other high-dimensional biomedical data.